Før man forstår B træ og B+ træ forskelle, bør vi kende B-træet og B+-træet separat.
Hvad er B-træet?
B træ er et selvbalancerende træ, og det er et m-vejs træ, hvor m definerer rækkefølgen af træet. Btree er en generalisering af Binært søgetræ hvor en node kan have mere end én nøgle og mere end to børn afhængigt af værdien af m . I B-træet er dataene specificeret i en sorteret rækkefølge med lavere værdier i venstre undertræ og højere værdier i højre undertræ.
java filter stream
Egenskaber af B-træ
Følgende er egenskaberne for B-træet:
- I B-træet skal alle bladknuderne være på samme niveau, hvorimod bladknuderne i tilfælde af et binært træ kan være på forskellige niveauer.
Lad os forstå denne egenskab gennem et eksempel.
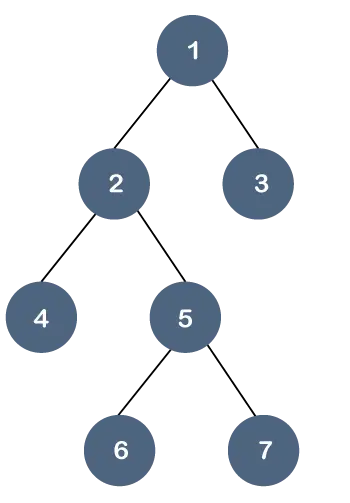
I ovenstående træ er alle bladknuderne ikke på samme niveau, men de har de yderste to børn. Derfor kan vi sige, at ovenstående træ er en binært træ men ikke et B-træ.
- Hvis B-træet har en rækkefølge på m, så kan hver node maksimalt have m Ved minimum børn har bladknuderne nul børn, rodknuden har to børn, og de indre noder har et loft på m/2.
- Hver node kan have maksimale (m-1) nøgler. For eksempel, hvis værdien af m er 5, så er den maksimale værdi af nøgler 4.
- Rodnoden har minimum én nøgle, hvorimod alle de andre noder undtagen rodknuden har (loft på m/2 minus - 1) minimumsnøgler.
- Hvis vi udfører indsættelse i B-træet, så indsættes noden altid i bladknuden.
Antag, at vi vil oprette et B-træ af orden 3 ved at indsætte værdier fra 1 til 10.
Trin 1: Først opretter vi en node med 1 værdi som vist nedenfor:

Trin 2: Det næste element er 2, som kommer efter 1 som vist nedenfor:

Trin 3: Det næste element er 3, og det indsættes efter 2 som vist nedenfor:

Da vi ved, at hver node maksimalt kan have 2 nøgler, vil vi dele denne node gennem det midterste element. Det midterste element er 2, så det flytter til sin forælder. Noden 2 har ikke nogen forælder, så den bliver rodknuden som vist nedenfor:

Trin 4: Det næste element er 4. Da 4 er større end 2 og 3, vil det blive tilføjet efter 3'eren som vist nedenfor:

Trin 5: Det næste element er 5. Da 5 er større end 2, 3 og 4, vil det blive tilføjet efter 4 som vist nedenfor:

Da vi ved, at hver node maksimalt kan have 2 nøgler, vil vi dele denne node gennem det midterste element. Det midterste element er 4, så det flytter til sin forælder. Forælderen er node 2; derfor vil 4 blive tilføjet efter 2 som vist nedenfor:

Trin 6: Det næste element er 6. Da 6 er større end 2, 4 og 5, så kommer 6 efter 5 som vist nedenfor:

Trin 7: Det næste element er 7. Da 7 er større end 2, 4, 5 og 6, så kommer 7 efter 6 som vist nedenfor:

Da vi ved, at hver node maksimalt kan have 2 nøgler, vil vi dele denne node gennem det midterste element. Det midterste element er 6, så det flytter til sin forælder som vist nedenfor:

Men 6 kan ikke tilføjes efter 4, fordi noden maksimalt kan have 2 nøgler, så vi deler denne node gennem det midterste element. Det midterste element er 4, så det flytter til sin forælder. Da node 4 ikke har nogen forælder, bliver node 4 en rodnode som vist nedenfor:

Hvad er et B+ træ?
Det B+ træ er også kendt som et avanceret selvbalanceret træ, fordi hver vej fra træets rod til træets blad har samme længde. Her betyder samme længde, at alle bladknuderne optræder på samme niveau. Det vil ikke ske, at nogle af bladknuderne forekommer på tredje niveau og nogle af dem på andet niveau.
Et B+-træindeks betragtes som et indeks på flere niveauer, men B+-træstrukturen ligner ikke de sekventielle sekventielle indeksfiler på flere niveauer.
Hvorfor bruges B+-træet?
Et B+ træ bruges til at gemme posterne meget effektivt ved at gemme posterne på en indekseret måde ved hjælp af den B+ træ indekserede struktur. På grund af indeksering på flere niveauer bliver dataadgangen hurtigere og nemmere.
B+ træ Nodestruktur
B+-træets nodestruktur indeholder pointere og nøgleværdier vist i nedenstående figur:

Som vi kan observere i ovenstående B+ træknudestruktur, at den indeholder n-1 nøgleværdier (k1til kn-1) og n pointer (s1til sn).
Søgenøgleværdierne, som er placeret i noden, holdes i sorteret rækkefølge. Således, hvis jeg
Begrænsning på forskellige typer knudepunkter
Lad 'b' være rækkefølgen af B+ træet.
Node uden blade
linux kørselskommando
Lad 'm' repræsentere antallet af børn i en node, så kan forholdet mellem rækkefølgen af træet og antallet af børn repræsenteres som:

Lad k repræsentere søgenøgleværdierne. Forholdet mellem rækkefølgen af træet og søgenøglen kan repræsenteres som:
Da vi ved, at antallet af pointere er lig med søgenøgleværdierne plus 1, så matematisk kan det skrives som:
Antal pointere (eller børn) = Antal søgetaster + 1
Derfor ville det maksimale antal pointere være 'b', og det mindste antal pointere ville være loftfunktionen for b/2.
Bladknude
En bladknude er en knude, der forekommer på det sidste niveau af B+-træet, og hver bladknude bruger kun én pointer til at forbinde med hinanden for at give den sekventielle adgang på bladniveauet.
I bladknude er det maksimale antal børn:

Det maksimale antal søgenøgler er:

Root Node
Det maksimale antal børn i tilfælde af rodknuden er: b
Minimumsantallet af børn er: 2
Særlige tilfælde i B+ træ
Case 1: Hvis rodknuden er den eneste knude i træet. I dette tilfælde bliver rodknuden til bladknuden.
I dette tilfælde er det maksimale antal børn 1, dvs. selve rodknuden, hvorimod minimumsantallet af børn er b-1, hvilket er det samme som for en bladknude.
Repræsentation af en bladknude i B+ træ

I ovenstående figur, '.' repræsenterer markøren, mens 10, 20 og 30 er nøgleværdierne. Markøren indeholder adressen, hvor nøgleværdien er gemt, som vist i ovenstående figur.
Eksempel på B+ træ

I ovenstående figur indeholder noden tre nøgleværdier, dvs. 9, 16 og 25. Den markør, der vises før 9, indeholder nøgleværdierne mindre end 9 repræsenteret af kjeg. Pointeren, der vises før 16, indeholder nøgleværdierne større end eller lig med 9, men mindre end 16 repræsenteret ved kj. Markøren, der vises før 25, indeholder nøgleværdierne større end eller lig med 16, men mindre end 25 repræsenteret af kn.
Forskelle mellem B-træ og B+-træ

Følgende er forskellene mellem B-træet og B+-træet:
| B træ | B+ træ |
|---|---|
| I B-træet er alle nøgler og poster gemt i både interne såvel som bladknuder. | I B+-træet er nøgler de indekser, der er gemt i de interne noder, og poster er gemt i bladknuderne. |
| I B-træ kan nøgler ikke lagres gentagne gange, hvilket betyder, at der ikke er nogen duplikering af nøgler eller poster. | I B+ træet kan der være redundans i forekomsten af nøglerne. I dette tilfælde er posterne gemt i bladknuderne, hvorimod nøglerne er gemt i de interne knudepunkter, så redundante nøgler kan være til stede i de interne knudepunkter. |
| I Btree er bladknuder ikke knyttet til hinanden. | I B+ træ er bladknuderne forbundet med hinanden for at give den sekventielle adgang. |
| I Btree er søgning ikke særlig effektiv, fordi posterne enten er lagret i blade eller interne noder. | I B+ træ er søgning meget effektiv eller hurtigere, fordi alle posterne er gemt i bladknuderne. |
| Sletning af interne noder er meget langsom og en tidskrævende proces, da vi også skal overveje barnet til den slettede nøgle. | Sletning i B+ træ er meget hurtig, fordi alle registreringerne er gemt i bladknuderne, så vi ikke behøver at overveje knudepunktets barn. |
| I Btree er sekventiel adgang ikke mulig. | I B+-træet er alle bladknuderne forbundet med hinanden gennem en pointer, så sekventiel adgang er mulig. |
| I Btree udføres jo flere flækkeoperationer på grund af hvilke højden stiger i forhold til bredden, | B+ træet har mere bredde sammenlignet med højden. |
| I Btree har hver node mindst to forgreninger, og hver node indeholder nogle poster, så vi behøver ikke at gå indtil bladknuderne for at få dataene. | I B+ træ indeholder interne noder kun pointere, og bladknuder indeholder poster. Alle bladknuderne er på samme niveau, så vi er nødt til at krydse til bladknuderne for at få dataene. |
| Rodknuden indeholder mindst 2 til m børn, hvor m er rækkefølgen af træet. | Rodknuden indeholder mindst 2 til m børn, hvor m er rækkefølgen af træet. |
